Data flow with pipe and solving a Roman numerals problem
 Photo by
Matt Hardy
Photo by
Matt Hardy
This is an interesting problem I encountered while solving some challenges in the Exercism site. The challenge is the idea of transforming a number into its roman numeral.
Some examples:
1 # => I
2 # => II
4 # => IV
27 # => XXVII
48 # => XLVIII
141 # => CXLI
575 # => DLXXV
1024 # => MXXIV
One idea to solve this problem is to transform each digit of the number and then join them together. To transform each digit, we need to know two pieces of information: the digit and if the digit is from the digit, dozens, hundreds, or thousands box.
To know that, we can use the help of an index. Let's see the algorithm:
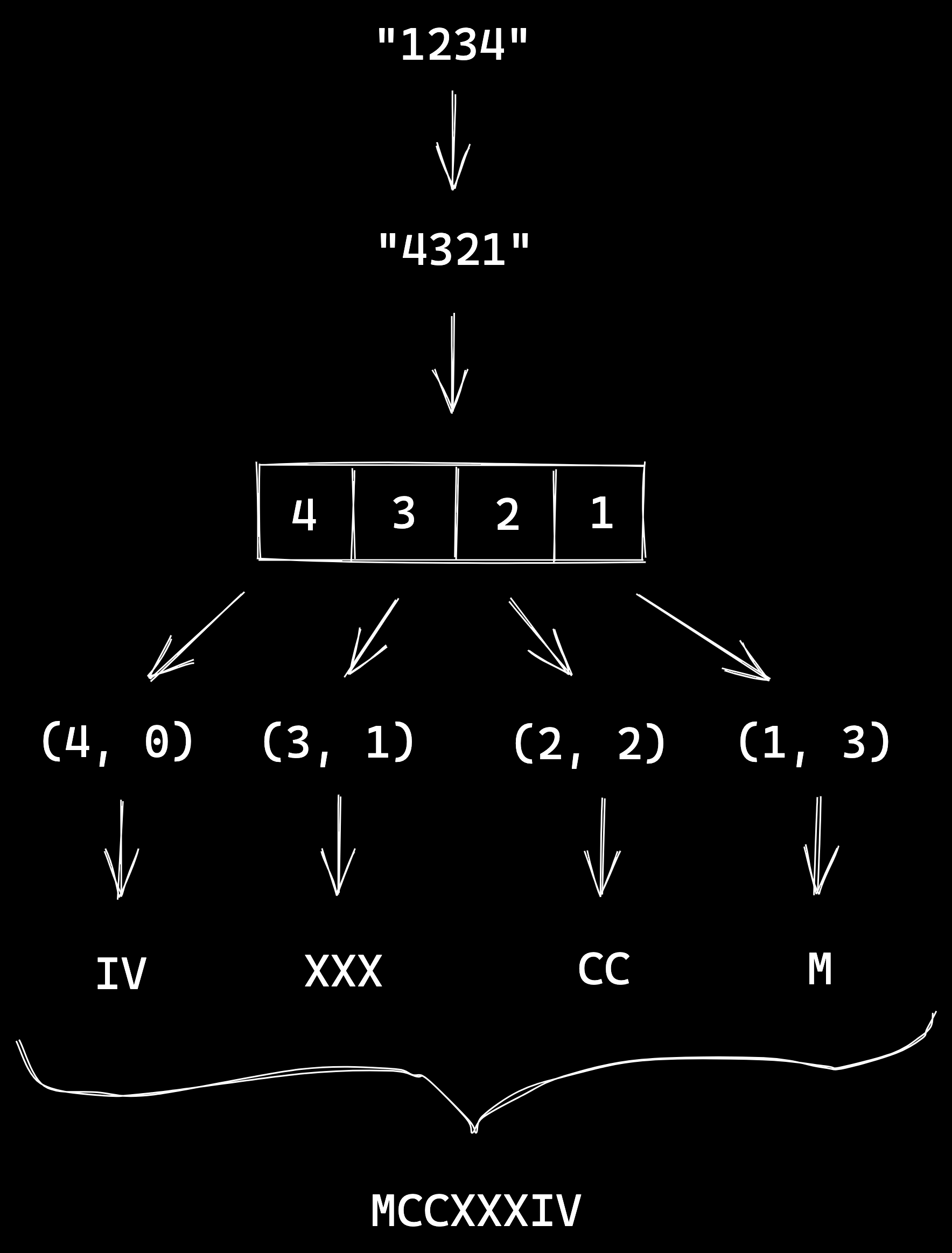
What are we doing here?
- Transform the integer to a string
- Reverse the string: we only reverse the string because we want to make it easier to use the index.
- Split string into a list of chars: transform the string into a list to reduce it.
- Reduce to build the roman numeral: for each digit, we use the digit and the index to map to a roman numeral and then concat them all.
To transform a number into a string, we can use the
Integer.to_string(), then we reverse the string with
String.reverse(), split each string character with the
String.split("", trim: true) function, and finally we can
use the reduce function to build the final roman string.
As I showed in the illustration above, we will use the index to know the type of the digit (digit, dozens, hundreds, thousands), and then map the roman numeral. To map from digit to roman, I created 3 maps:
- for digit
@digit_to_roman %{
"0" => "",
"1" => "I",
"2" => "II",
"3" => "III",
"4" => "IV",
"5" => "V",
"6" => "VI",
"7" => "VII",
"8" => "VIII",
"9" => "IX"
}
- for dozens
@dozens_to_roman %{
"0" => "",
"1" => "X",
"2" => "XX",
"3" => "XXX",
"4" => "XL",
"5" => "L",
"6" => "LX",
"7" => "LXX",
"8" => "LXXX",
"9" => "XC"
}
- for hundreds
@hundreds_to_roman %{
"0" => "",
"1" => "C",
"2" => "CC",
"3" => "CCC",
"4" => "CD",
"5" => "D",
"6" => "DC",
"7" => "DCC",
"8" => "DCCC",
"9" => "CM"
}
- for thousands
@thousands_to_roman %{
"0" => "",
"1" => "M",
"2" => "MM",
"3" => "MMM",
"4" => "MMMM"
}
Now we can implement a simple function to use the index to choose which map it'll use:
defp to_roman(digit, index) do
case index do
0 ->
@digit_to_roman[digit]
1 ->
@dozens_to_roman[digit]
2 ->
@hundreds_to_roman[digit]
3 ->
@thousands_to_roman[digit]
end
end
And finally, the reducer function to build the roman numeral string:
defp build_roman_numeral({string_digit, index}, roman) do
to_roman(string_digit, index) <> roman
end
The flow looks like this:
def numeral(number) do
number
|> Integer.to_string()
|> String.reverse()
|> String.split("", trim: true)
|> Enum.with_index()
|> Enum.reduce("", &build_roman_numeral/2)
end
And the code looks like this:
defmodule RomanNumerals do
@digit_to_roman %{
"0" => "",
"1" => "I",
"2" => "II",
"3" => "III",
"4" => "IV",
"5" => "V",
"6" => "VI",
"7" => "VII",
"8" => "VIII",
"9" => "IX"
}
@dozens_to_roman %{
"0" => "",
"1" => "X",
"2" => "XX",
"3" => "XXX",
"4" => "XL",
"5" => "L",
"6" => "LX",
"7" => "LXX",
"8" => "LXXX",
"9" => "XC"
}
@hundreds_to_roman %{
"0" => "",
"1" => "C",
"2" => "CC",
"3" => "CCC",
"4" => "CD",
"5" => "D",
"6" => "DC",
"7" => "DCC",
"8" => "DCCC",
"9" => "CM"
}
@thousands_to_roman %{
"0" => "",
"1" => "M",
"2" => "MM",
"3" => "MMM",
"4" => "MMMM"
}
def numeral(number) do
number
|> Integer.to_string()
|> String.reverse()
|> String.split("", trim: true)
|> Enum.with_index()
|> Enum.reduce("", &build_roman_numeral/2)
end
defp build_roman_numeral({string_digit, index}, roman) do
to_roman(string_digit, index) <> roman
end
defp to_roman(digit, index) do
case index do
0 ->
@digit_to_roman[digit]
1 ->
@dozens_to_roman[digit]
2 ->
@hundreds_to_roman[digit]
3 ->
@thousands_to_roman[digit]
end
end
end
It's so fun to think in functional programming when solving a problem.